The Hominidae (/hɒˈmɪnɨdiː/), also known as great apes,[notes 1] or hominids, form a taxonomic family of primates, including four extant genera: orangutans (Pongo) with two species extant; gorillas (Gorilla) with two species; chimpanzees (Pan) with two species; and humans (Homo) with one species.[1]
Several revisions over time in classifying the great apes have caused a varied use of the word hominid. Its original meaning referred only to humans (Homo) and their closest relatives; that restrictive meaning now is largely assumed by the term “hominin”, which comprises all members of the human clade after the split from the chimpanzees. The modern meaning of “hominid” refers to all the great apes including humans. However, usage still varies, and some scientists and laypersons may still use the term in the traditional, more restrictive, meaning; the scholarly literature generally will show the traditional usage until around the turn of the 21st century.
In the early Miocene, about 22 million years ago, there were many kinds of arboreally adapted primitive catarrhines from East Africa; the variety suggests a long history of prior diversification. Fossils at 20 million years ago include fragments attributed to Victoriapithecus, the earliest Old World Monkey. Among the genera thought to be in the ape lineage leading up to 13 million years ago are Proconsul, Rangwapithecus, Dendropithecus, Limnopithecus, Nacholapithecus, Equatorius, Nyanzapithecus, Afropithecus, Heliopithecus, and Kenyapithecus, all from East Africa.
At sites far distant from East Africa, the presence of other generalized non-cercopithecids, that is, non-monkey primates, of middle Miocene age—Otavipithecus from cave deposits in Namibia, and Pierolapithecus and Dryopithecus from France, Spain and Austria—is further evidence of a wide diversity of ancestral ape forms across Africa and the Mediterranean basin during the relatively warm and equable climatic regimes of the early and middle Miocene. The most recent of these far-flung Miocene apes (hominoids) is Oreopithecus, from the fossil-rich coal beds in northern Italy and dated to 9 million years ago.
Molecular evidence indicates that the lineage of gibbons (family Hylobatidae), the lesser apes, diverged from that of the great apes some 18–12 million years ago, and that of orangutans (subfamily Ponginae) diverged from the other great apes at about 12 million years. There are no fossils that clearly document the ancestry of gibbons, which may have originated in a still-unknown South East Asian hominoid population; but fossil proto-orangutans, dated to around 10 million years ago, may be represented by Sivapithecus from India and Griphopithecus from Turkey.[5]
A reconstruction of a female Australopithecus afarensis (National Museum of Natural History)
Species close to the last common ancestor of gorillas, chimpanzees and humans may be represented by Nakalipithecus fossils found in Kenya and Ouranopithecus found in Greece. Molecular evidence suggests that between 8 and 4 million years ago, first the gorillas (genus Gorilla), and then the chimpanzees (genus Pan) split off from the line leading to the humans. Human DNA is approximately 98.4% identical to that of chimpanzees when comparing single nucleotide polymorphisms (see human evolutionary genetics). The fossil record, however, of gorillas and chimpanzees is limited; both poor preservation—rain forest soils tend to be acidic and dissolve bone—and sampling bias probably contribute most to this problem.
Other hominins probably adapted to the drier environments outside the African equatorial belt; and there they encountered antelope, hyenas, dogs, pigs, elephants, horses, and other forms becoming adapted to surviving in the East African savannas, particularly the regions of the Sahel and the Serengeti. The wet equatorial belt contracted after about 8 million years ago, and there is very little fossil evidence for the divergence of the hominin lineage from that of gorillas and chimpanzees—which split was thought to have occurred around that time. The earliest fossils argued by some to belong to the human lineage are Sahelanthropus tchadensis (7 Ma) and Orrorin tugenensis (6 Ma), followed by Ardipithecus (5.5–4.4 Ma), with species Ar. kadabba and Ar. ramidus.
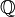 ,
, if and only if
if and only if 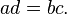
 if and only if
if and only if 


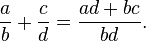

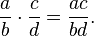



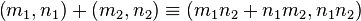

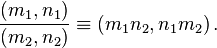
![\cdots = [(-2m,-2n)] = [(-m,-n)] = [(m,n)] = [(2m,2n)] = \cdots.](https://upload.wikimedia.org/math/6/3/2/632e35ae4f8071ee9310c1b745a837b0.png)


 are positive), we have
are positive), we have





